＜2022年県立御三家入試分析会編＞Vol.２_数学の問題を分析

　今回は数学です。数学は２週に分けて、それぞれ注目すべき問題を分析します。

令和４年度入試の問題は

⇒こちら（リンク先は埼玉県教育委員会HPです）

　令和４年度の問題には、いくつかの特徴がありますが、出題の傾向や考え方がこれまでと大きく変わったかと言われるとそういうわけではありません。
　数学も英語と同様、新たに加わった単元があります。代表的なのは四分位数と呼ばれるデータの活用についての内容です。今回の箱ひげ図の問題は簡単でした。つまり、その内容をしっかりと取り組んでいた人であれば全員できたと思います。新出単元というのはこれからも出てきますので、しっかりと対策を講じる必要があります。

　それでは実際に出題された問題を見ていきます。

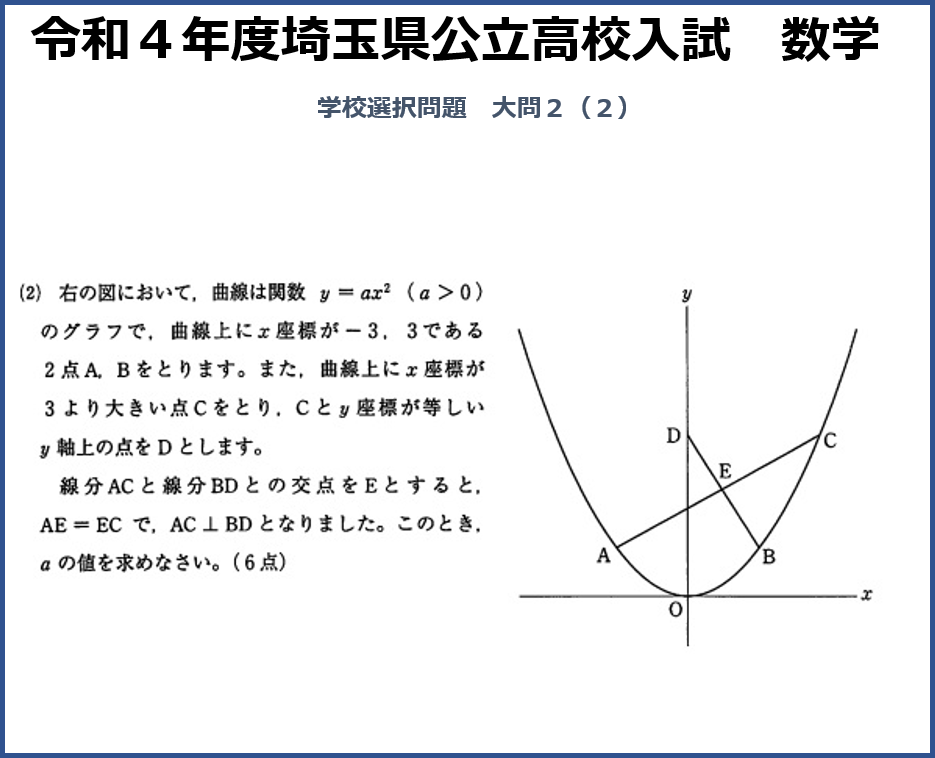
　これは放物線というもので、中学３年生の学習内容です。中学２年生までの学習では解けない問題ですが、どういう構成で問題ができあがっているのか紹介します。
　この問題の求める値はaの値です。一見すると入試対策を進めてきた受験生はできそうな感覚になります。ところが、正解に至るまでの過程はとても長いです。いくつもの知識を使い、多くのステップを踏まなければいけません。この問題の最大の特徴は、何かに気付く、見つけることが必要だということです。

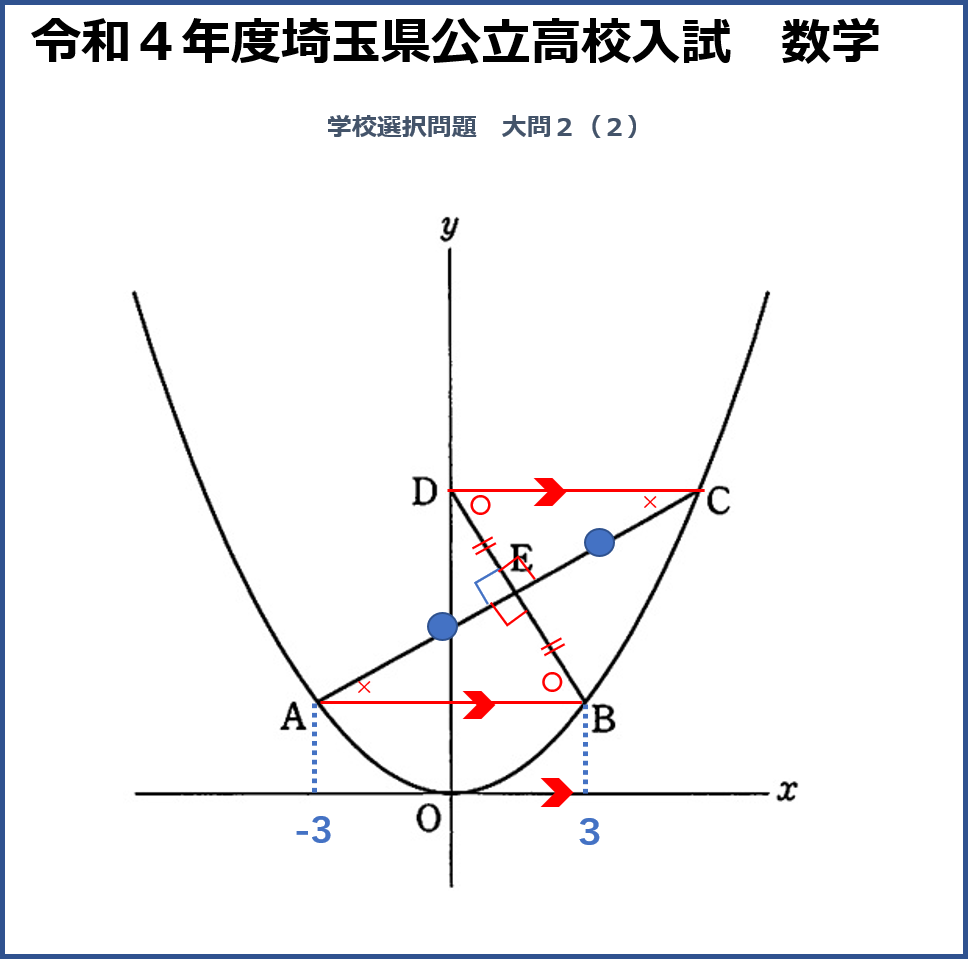
　この問題の気付くべき点は、条件を読んでDCとABはx軸に平行ということです。次に、平行であり、Eが中点ということは、ABEの三角形とCDEの三角形は合同であることに気付いてください。詳しい合同条件は省略しますが、問題文に示されていなくても合同であるということに気付かなければいけません。

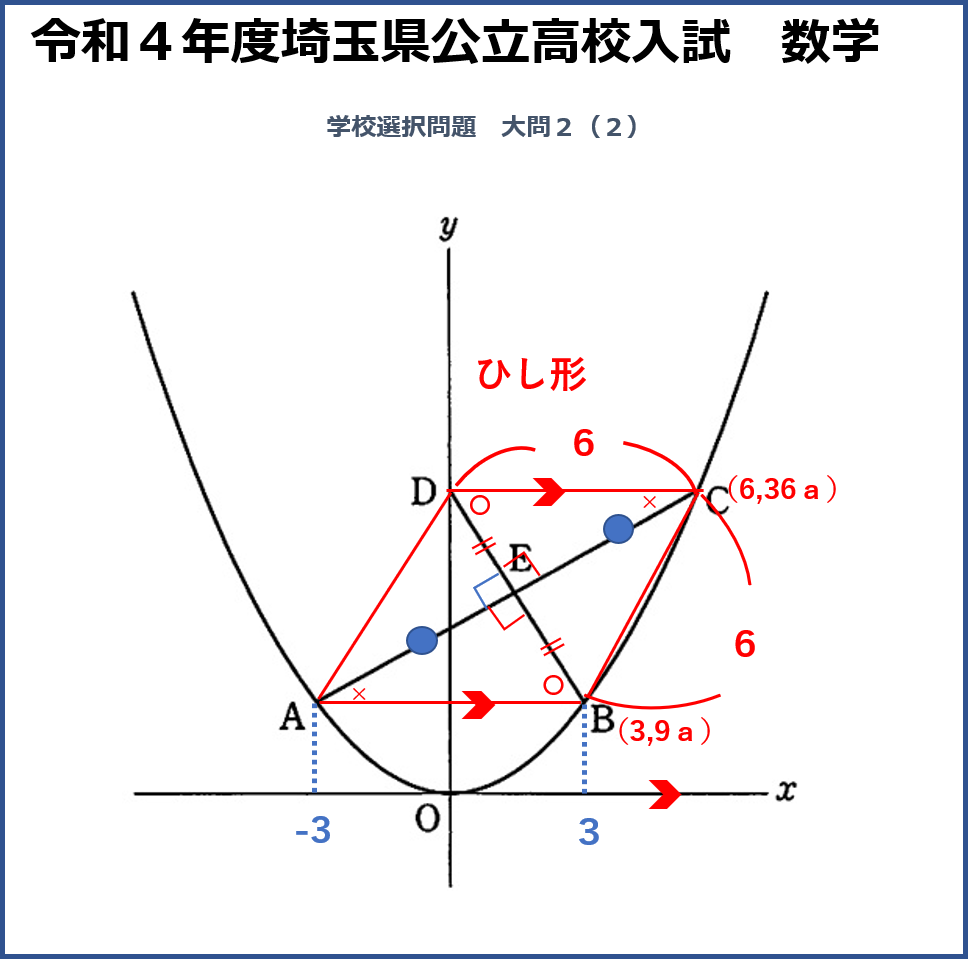
　そしてＡＢ、ＢＣ、ＣＤ、ＤＡを線で結ぶと平行四辺形が出来上がるということ、そして問題に出された条件を踏まえて、対角線が垂直に交わるので、この平行四辺形がひし形であるということ、ここまで見抜くことがこの問題の最大のポイントです。ここまで３段階、平行、合同、平行四辺形というステップを踏まえて「ひし形」を導き出しました。ここまで分からないと、ａを求めるのは困難です。

「ひし形」が分かれば４つの辺は等しいということが分かるので、線ＢＣ、ＣＤの長さは６。曲線の関数は※１なのでＢ（３，９ａ）、Ｃ（６、３６ａ）です。次に式を立てます。これは中学３年生の後半で学習する内容を使います。

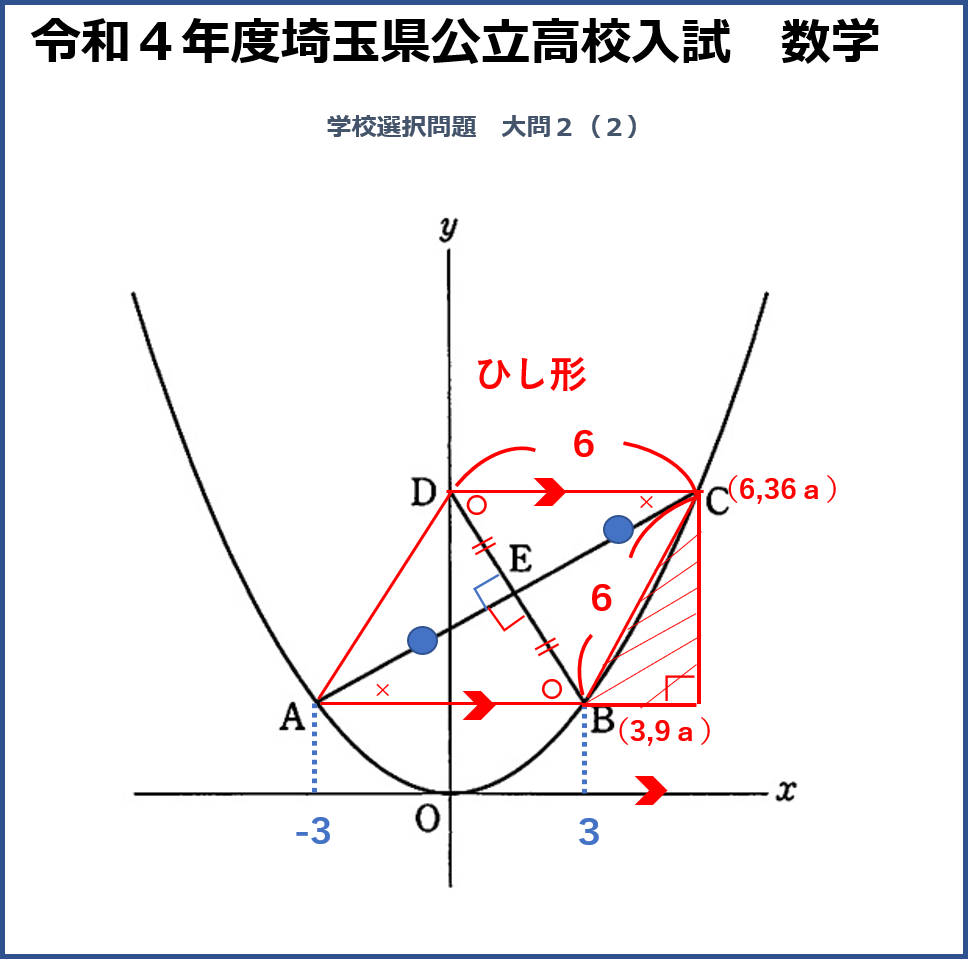
　Ｃからｘ軸に向かって垂直に線を引き、Ｂからｘ軸と平行に線を引き、つなげると直角三角形が出来上がります。すると三平方の定理を使うことができます。ここまできてようやくａの値が求められます。これらのステップを一つでも途絶えてしまうと解答にたどり着けません。
　もちろん、今説明した方法以外の解き方もあります。垂直に交わるということは傾きの積が－１になる、ということを知っていればそれを使った導き方もできます。この考え方でも数多くのステップを踏まないと解答できないことに変わりません。

　今年の入試の特徴、続いては抽象化です。物事を文字で判断する、検証していくということが大きくクローズアップされていました。次の問題を見て説明していきます。

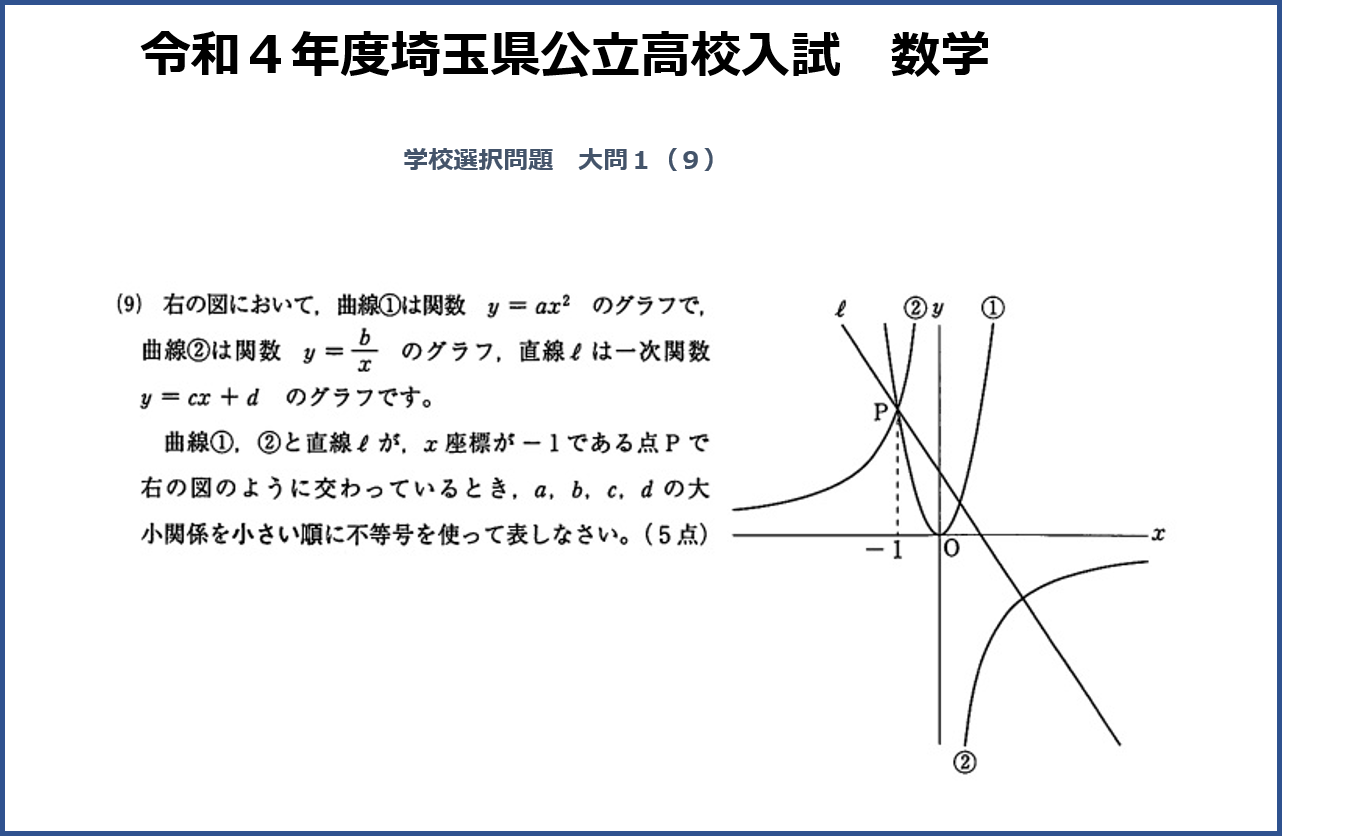
　一次関数の直線のグラフｙ＝ｃｘ+ｄ、放物線の関数のグラフ※２、反比例のグラフ※３この状態の中でａ、ｂ、ｃ、ｄの大きさを比較し、小さい順に並べ替えるという問題。値は問われていません。理論的に考えてどういう順に並びますか、それを解明してくださいと言っています。

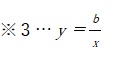
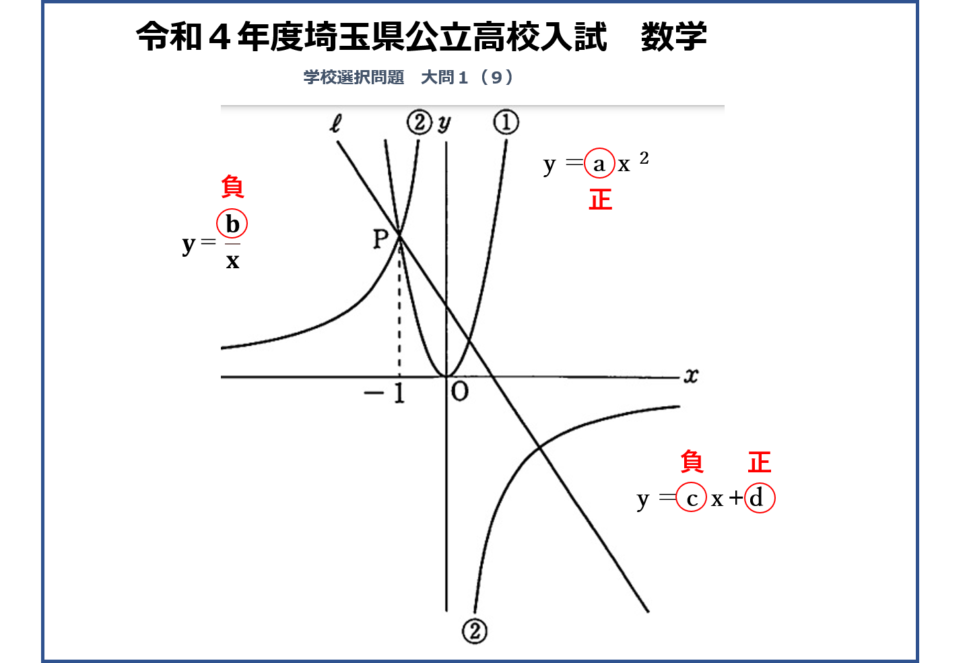
　ぱっと見、捉えどころのない問題だと感じると思います。簡単に判断できる部分は、放物線というグラフの特徴から、上に向かって伸びているのでaは正の値だということです。次に反比例のグラフの位置からｂは負の値です。　そして直線ℓは右下がりなのでｃは負。ｄはｙ軸との接点をみて正。続いては、正の値のａとｄはどちらが大きいのか、ｃとｂはどちらが大きいのかを求めていきます。要領のいい受験生であれば、仮にａの値を２にしてみるとＰ（－１，２）、※４なのでｂの値は－2。

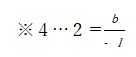
　また、直線ℓとy軸の接点を仮に０．５にしてみるとｃは傾きなので－１．５。

　そうすると小さい順にｂ、ｃ、ｄ、ａと並べることができます。この問題は値ではなく順番を聞いているので、苦肉の策としてこういった具体的な数字を試してみることで解答できます。しかし、これが「順番に並べなさい。その際、途中の説明もきちんと書きなさい」という問題だったとすると今のような解答では、採点方法によっては１点ももらえない可能性があります。ですので、これから３年生で放物線を習うと思いますが、学習が終わった後は、答えを出すだけでなく、途中の説明を書くという過程も１つ１つの問題で練習すると良いと思います。

=スクール21入試情報センター「2022年県立御三家入試分析会編」より=

☆次回は、６月９日に
コラム「数学の問題を分析（２）」を配信します。

【関連コラム】

2022年県立御三家入試分析会編

Vol.１_英語の問題を分析

2022年高校入試報告会編