＜2022年県立御三家入試分析会編＞Vol.３_数学の問題を分析(2)

＜数学の問題を分析（１）は→こちらから＞
　

　続いての問題は大問３です。

　この問題は先生と生徒の会話を読んで問に答えていく問題です。

令和４年度入試の問題は

⇒こちら（リンク先は埼玉県教育委員会HPです）

　読んでみると会話の中に問題の条件が書かれています。試験時間は限られているので、ずらっと書かれた会話文の中から的確に条件を読み取らなければなりません。
ここでは（１）の確率の問題に注目し、詳しく解説してみます。

　後半の大問３や４では平面図形、空間図形、関数などは多いですが、確率の問題が大問一題分まるまる出題されるということは稀です。この問題は、さいころを２回投げるという確率の典型的な問題でした。しかし、条件の提示が変わっているので、受験生によっては、見たことのない問題に見えてしまうこともあったかもしれません。
　ただし、落ち着いて、今まで解いてきたどの問題と同質なのかをしっかりと判断できれば難しくはありません。
　この問題の難しさは他にもあります。確率なので中学２年生で学習する内容です。ところが会話文に「円の性質を利用すると」という内容が出てきます。ここで必要な知識は、「円周角」です。直径に対する円周角は直角であるということを中学３年生で勉強しますが、それが会話の中に出てきています。つまり中学２年生の知識と３年生の知識を融合しないと解けないということです。異なる単元の知識を結び合わせることが重要です。それ自体は珍しくありませんが、長い問題文や確率にしては珍しい問題です。

　１つ１つ調べていってもできなくない数ですが、会話の中の条件を読むと出てくる「円の性質を利用すると」いいということですね。実際に円を描いてみると６カ所が該当することが分かります。

　さいころ２つの確率の問題だと分母が３６になりますが（３）の問題では、
「三角形になる」という条件が付けくわえられています。
詳しい解説はしませんが、図を見るとAは、（２，１）、Ｂは、（４，５）なのでちょうど中間の（３，３）にＰがくると、そもそも三角形ができません。あるいは、Ｐが（２，１）と（４，５）でも三角形はできません。この３通りを除くことが分かるので、分母は３３に変化します。

　続いて大問４を見ていきます。

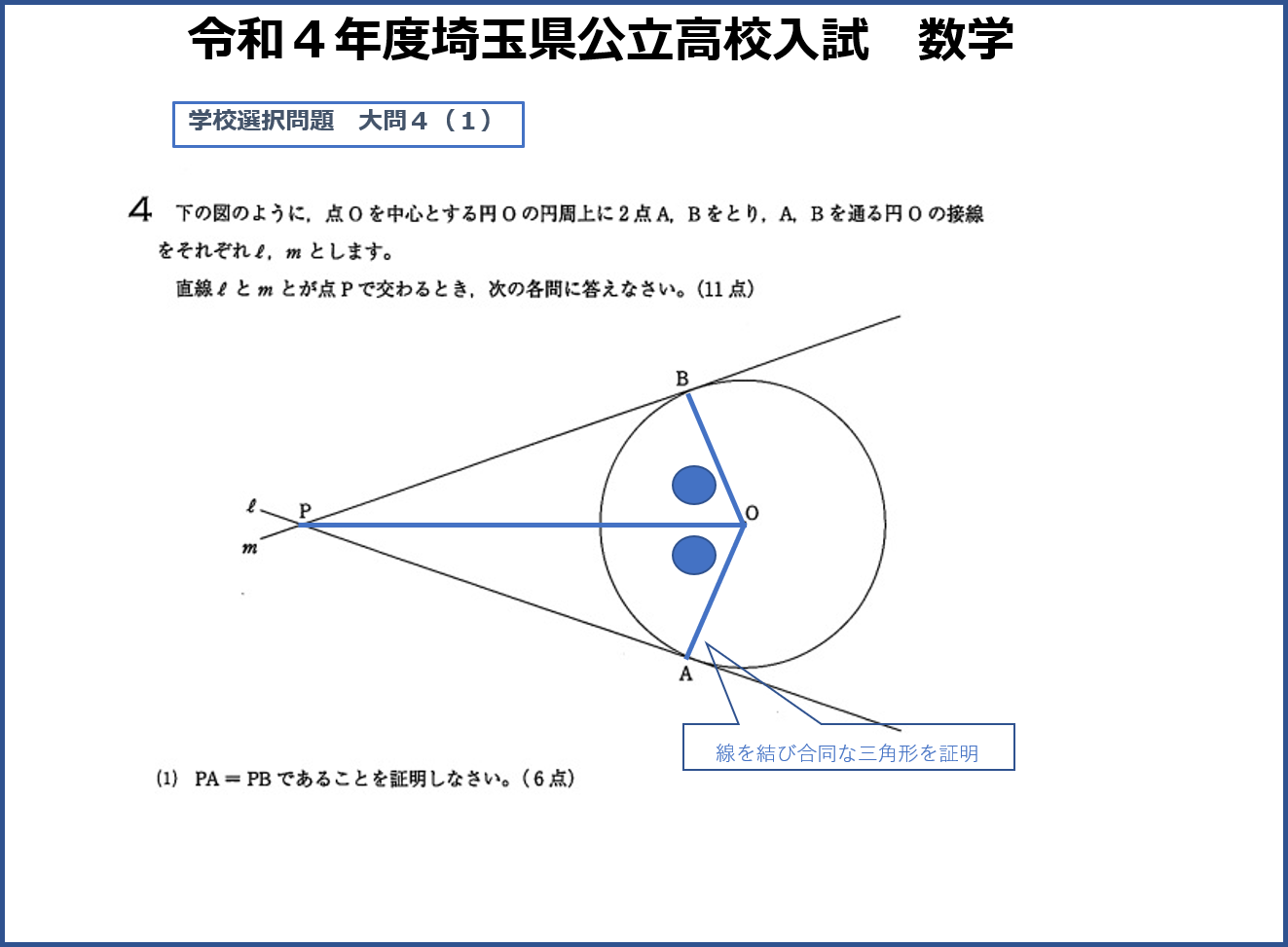
　（１）は円と接線の性質について学習していますので、なぜそうなるのか説明すればいい簡単な問題です。
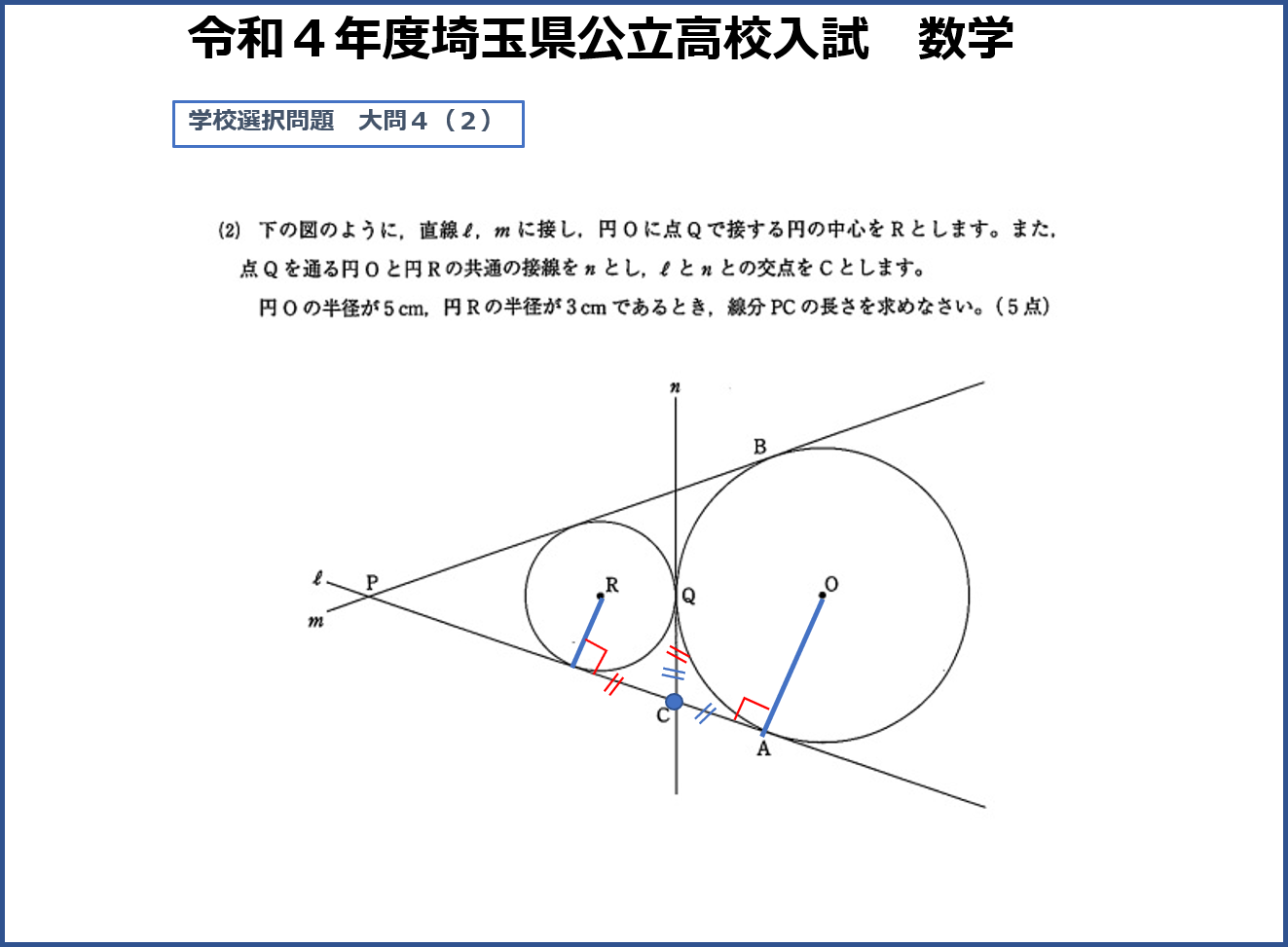
　それに比べ（２）は難易度がかなり上がります。（１）の図形に円と接線が１つずつ追加されています。図形の基本は中学１年生で勉強しますが、さらに深い知識は中学校３年生の「円の断面」という単元で学びます。条件としては大きい円の半径が５センチ、小さい円の半径３センチであるときの線分ＰＣの長さです。これを解くには中学３年生の内容も含まれていますので、まだ分からなくても大丈夫ですが、解説を読んで、色々な段階を踏まえないと解けないということを知っておいてください。

　まず（１）でＰＡとＰＢが等しいということを証明しましたが、（２）の図形にはこの性質の部分がたくさんあります。この性質を探すと、

直線ℓと円Ｒの接点からCと、QからCまでの長さが等しいこと
円Ｏの接線であることからＣＱ=ＡＣであること

　以上のことから直線ℓと円Ｒの接点からAの中点がＣであることが分かります。
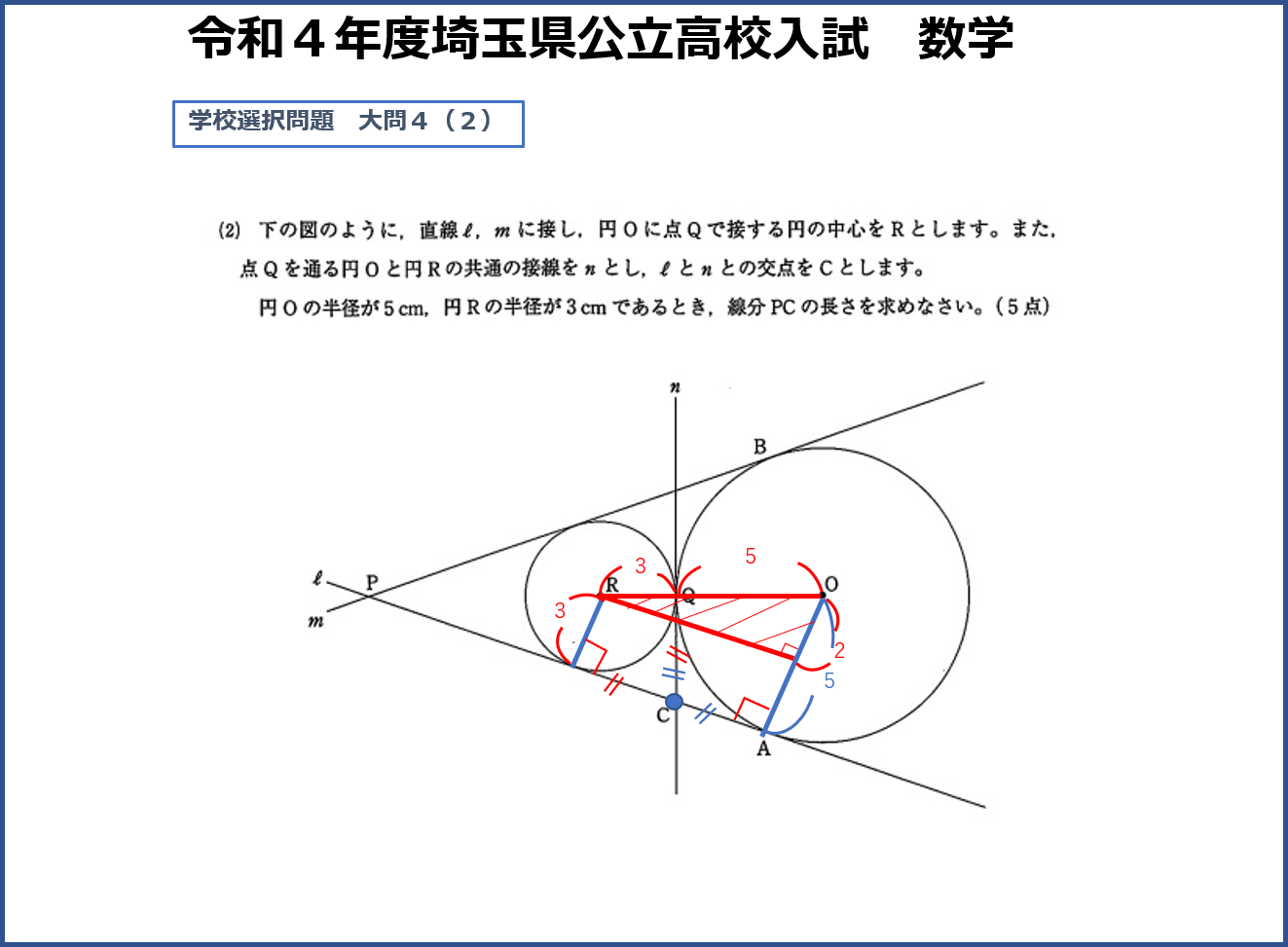
　では、ＰＣの長さはどう求めるのか。具体的な長さが分かっているのは円の半径だけです。これを使うとどこの長さが求められるかを考えます。ここで知っておいていただきたい数学のテクニックは「接点があったら結んで90度にする」ということです。

　そして「２つの円が接していたら中心を打つ」ことも知っておきましょう。すると、台形ができるので、この台形を長方形と直角三角形に分けます。直角三角形の部分で「三平方の定理」を使うと辺の長さが求められます。これは直線ℓと円Ｒの接点からＡの距離も求められたということです。しかし、このまま「三平方の定理」を使ってＰＣは求めることができるでしょうか。実はそう簡単にはいきません。

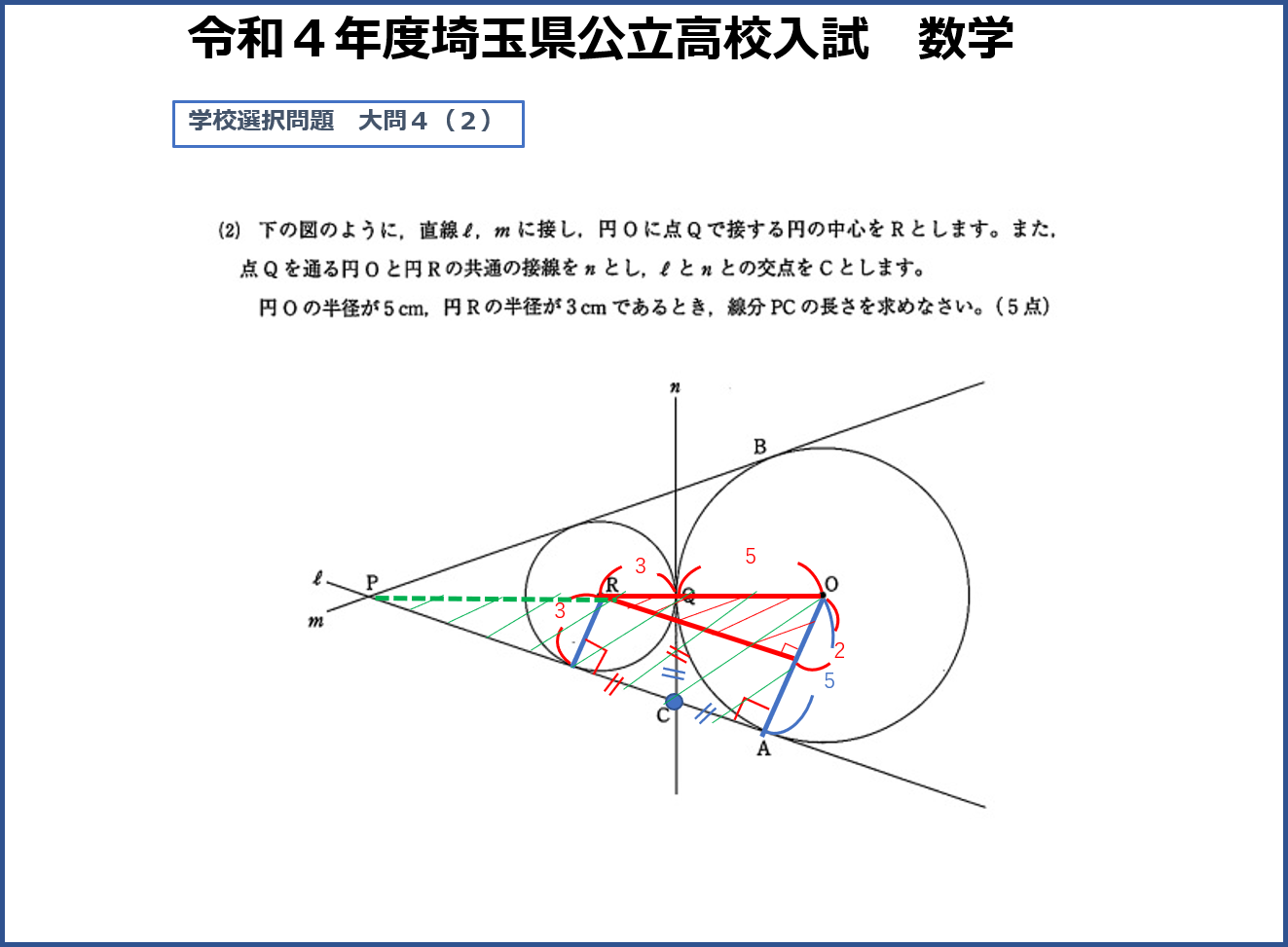
　ＰＡの長さかＰから円Rの接点までの長さが分からなければいけないということで、元々の図形が線対称なので対称軸で分けると△AOPの直角三角形ができます。先ほど台形から分けた直角三角形と今できた△AOP、これは「相似」の関係です。

　この相似の図形は小学校６年生で習った「拡大図と縮図」の発展した内容で、中学３年生で学習します。これを使ってＰＡの長さを求め、ＣＡの長さを引くことでＰＣの長さになります。
　一つ一つは難しくありませんが、解答までの工程がとても多いです。知識を組み合わせて何ができるか自分で判断する力が求められます。

　例えば、これが各工程について小問で「こことここの長さが等しいことを証明してください」「ここの長さを求めてください」と導くような出題であれば解答は簡単だったと思います。しかし、この問題は次に自分が見るべき場所はどこか、それを条件の中から紡ぎ出すということが大事なポイントになります。それが中学３年生の後半、入試対策をする上で大切になってくることです。

　最後におまけの話をします。

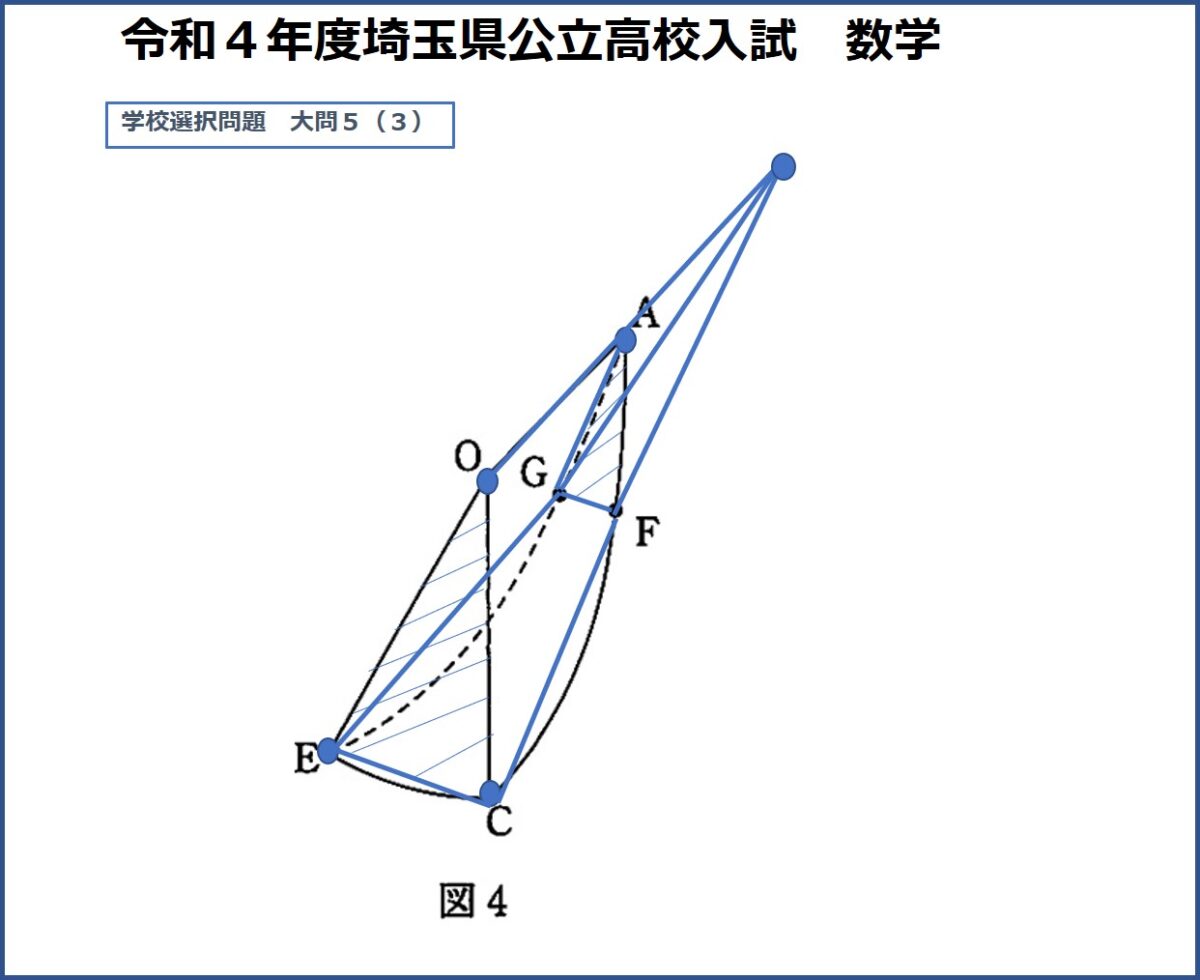
　今年の入試はとりわけ難しい問題が出ました。「カットされたスイカから考えました」とありますが、これはつまり球を切断した「空間図形」の問題です。先ほど問題の抽象化について話しましたが、この問題も半径をｒセンチとしています。文字式で計算を進める正確な判断力、思考力が必要だということです。
特に（３）は立体Ｖをさらに３分割した上に五面体を作って体積を求めるという、飛びぬけて難しい問題でした。立体の体積を直接計算できるのは球、すい形、柱形です。この３種類のどれを使うのだろうと考えるわけですが、そもそもこの五面体がどういう図形か分からないという受験生も少なくなかったと思います。三角形２つの面の周りに四角形の面が３つある形になります。形が分かったら次はどう求めればいいのか。

　ＯＡ，ＣＦ、ＥＧを伸ばしてみてください。ＯＥＣを底面に持つ大きな三角錐が出来上がります。

　そこからＡＧＦを底面に持つ三角錐の体積を引くことで五面体の体積が求められます。三角錐の体積は面積や比率、「三平方の定理」を使って解いていきます。また、「体積比」も使いますから非常にハードルの高い問題でした。なんとなくこれくらい、では求められない※１立方センチメートルという答えです。

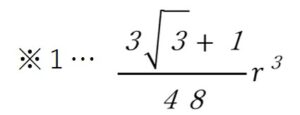
　過去問の学習をしていくと難易度の高い問題、とても基礎的で標準的な問題の両方に遭遇すると思います。埼玉県の特徴として、一つ一つの問題の差が激しいということが言えます。その中で合格ラインに必要な点数をどうやって取るかが入試対策で重要になってきます。
　今回は数学と英語、特に難しかった数学の問題を説明しましたが、入試対策をしていく上では基礎的な問題から全ての問題にきちんと取り組んでください。
　最後の三角すいの問題は、極端に難易度が高く、できなくても合否の判定にほとんど影響がなかった可能性が高いです。それは他の受験生もほとんどできていなかったと思われるからです。ですが、これから学習を進めていく上ではこういった問題もきちんと対処して、問題の種類を知り、解き方、難しさを学んでください。そうしないと入試本番で「これはできなくても合否に影響がないな」「これは絶対正解しないといけないな」「この問題は勝負どころだ」という難易度の判断ができません。
　本番に必要なのは解く力の有無だけではありません。一つ一つの問題のレベルをある程度見抜く力も大切です。それを身につけるためには本番でたとえできなくてもいいと思う問題でも対策を講じることがポイントです。

=スクール21入試情報センター「2022年県立御三家入試分析会編」より=

☆次回は、６月16日に
コラム「学習の効率化とは？」を配信します。

＜2022年県立御三家入試分析会編＞は、次回が最終回となります。

【関連コラム】

2022年県立御三家入試分析会編

2022年高校入試報告会編